My Maths Notes

maths notes suitable for A-level students and 1st year university students

The aim of this page

I am in the process of writing complete notes on the topics listed below. The level of these notes are/will be suitable for both A-level students and 1st year university students. Note that not all parts of the A-level syllabus for each topic are covered in my notes.

The topics I will inlude will be on Functions, Algebra, Differentiation, Integration, Series, and Complex Numbers.

In these notes I have tried / will try to do three things which are not often seen in textbook of maths at this level:

to provide detailed conceptual explanations of things whose understanding are often taken for granted;
to introduce variations on each topic in order to broaden and deepen one's learning of the topic being studies. Such variations are (virtually) never seen in standard textbooks, but can certainly be understood by A-Level and 1st year undergrad students. They taken from certain mathematics journals such as Mathematical Gazette, Two-Year College Mathematics Journal, Mathematical Spectrum, Mathematics Teacher, etc.;
to include as many diagrams as possible throughout in order to visualise the mathematics or concept being discussed;

(it is for these reasons that my notes are significantly longer, and the file size significantly larger, than is usual for notes of these types).

It is because of these three aspects that I believe that the notes below will be useful for 1st year university students studying maths, as well as A-level students.

If you have any questions about thing you do not understand and/or other ways of visualising something I have written I would be interested to know about it. You can contact me here about this.

What is available for download

Two types of material are available for download: notes and examples. In terms of notes, I have provided two versions: the first is complete version of the notes. As I have tried to develop each subject in a very integrated and coherent manner I suggest you read these notes.

However, if you are only interested in certain topics I have also included notes for each section as separate downloads. These notes make references to other sections, so you will need to refer to those other section if necessary in order to follow the flow of ideas within a given section.

Complete set of notes

Complete set of examples

On functions as transformations and the transformations of functions

(43p, 1.29Mb)

None

All examples are in the notes

Notes by section	Examples by section
1.1: Function as transformations (10p, 331Kb)	None
1.2: Describing the behaviour of f(x) under certain transformations (18p, 588Kb)	None
1.3: One complete example (5p, 113Kb)	None
1.4: How to indentify a function from a graph (12p, 434Kb)	None
1.5: Summary (2p, 45.7Kb)	None

Trigonometry I: Complete set of notes

Complete set of examples

On defining trigonometric ratios and functions (120p, 5.54Mb, )

None.

All examples are in the notes

Notes by section	Examples by section
Sec 1.1: Introduction Sec 1.2: Trig ratios: Using special triangles as a way of defining six new things about right-angled triangles (5.54Mb, 122p)	none
Sec 1.3: Relationships between the trig ratios: The beginning of trig identities none(3.31Mb, 17p)	none
Sec 1.4: Using a frame of reference to extend the use of trig ratios (362Kb, 25p)	none
Sec 1.5: Trig functions: The unit circle as a way of defining sin, cos, and tan (1.74Mb, 59p)	none
Sec 1.6: Non-circular functions (214Kb, 5p)	none

Hyperbolic functions: Derivation of sinh and cosh

These notes present a complete derivation of the hyperbolic trig functions sinh and cosh. I wrote these notes based on an amalgamation of notes from other sources, sources which I will referende in due course. The proof is based on the concepts of areas under curves, polar coordinates and rotation of axes (matrices).

Complete set of notes

Complete set of examples

Description to come

to come

Notes by section

Examples by section

to come

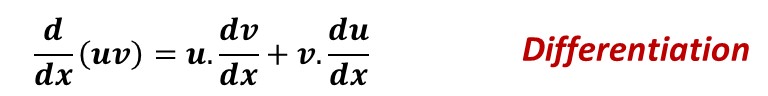
Differentiation I: Complete set of notes

Complete set of examples

On the definition of the derivative

and the proof of some basic derivatives (1.48Mb, 104p)

to come

Differentiation I: Notes by section	Examples by section
1.1: Introduction; 1.2: The derivatives as the slope of the curve at a point (393Kb, 21p)	to come
1.3: The derivatives as a function representing the slope of the curve as a whole (322Kb, 14p)	to come
1.4: On the formal definition of the derivative (119Kb, 5p)	to come
1.5: The derivative of x^n from 1st principles (96Kb, 4p)	to come
1.6: The derivatives as a transformation from position to slope	to come
1.7: The derivatives as a measure of sensitivity (139Kb, 7p)	to come
1.8: The derivatives as a measure of distribution (266Kb, 12p)	to come
1.9: The second derivative and beyond (to come)	to come
1.10: Equations involving the derivative in nature: Selected examples	to come
1.11: The derivative of other basic functions from 1st principles (342 Kb, 26p)	to come
1.12: Not all functions have derivatives (376Kb, 14p)	to come
1.13: Studies on derivatives and tangents (to come)	none

Differentiation II: Complete set of notes	Complete set of examples
On the rules of differentiation - to come	click here (2.46Mb, 51p)

Differentiation II: Notes by section	Examples by section
1.1: Introduction; 1.2: The multiplication by a constant rule	to come
1.3: The addition and subtraction rule	to come
*1.4: On the product rule for differentiation: d(u.v)/dx*	click here (366Kb, 7p)
1.5: *On the quotient rule for differentiation: d(u/v)/dx*	click here (211Kb, 4p)
1.6: On the chain rule for differentiation: d(f(g(x)))/dx	click here (215Kb, 5p)
1.7: Implicit differentiation	click here (293Kb, 8p)
1.8: Studies in differentiation	click here for set 1 (444Kb, 5p) click here for set 2 (222Kb, 6p)
1.9: More difficult examples on differentiation	click here (672Kb, 15p)

Complete set of notes	Complete set of examples
to come	to come

Notes by section	Examples by section
to come	to come
to come	to come
to come	to come

Complete set of notes	Complete set of examples
to come	to come

Notes by section	Examples by section
to come	to come
to come	to come
to come	to come

Complete set of notes	Complete set of examples
Complex numbers 1 - part 1 (2.65Mb, 149p)	See notes
Complex numbers 1 - part 2 (2.22Mb, 112p)	See notes

Notes by section	Examples by section
to come	to come
to come	to come
to come	to come